Normalizing flows, popularized by (Rezende, & Mohamed, 2015), are techniques used in machine learning to transform simple probability distribution functions into complicated ones. One of the popular use cases is in generative modelling - an unsupervised learning method - where the goal is to model a probability distribution given samples drawn from that distribution.
Why bother about normalizing flows?
-
They have been used in many TTS (text-to-speech) models, memorably in the Parallel WaveNet model (2017) where a clever application of normalizing flows resulted in a 1000 times faster generation of audio samples in comparison to the original WaveNet model. The Parallel WaveNet model was also deployed on Google assistant for real-time generation of audio.
-
Normally a back-propagation pass requires the activation value for each neuron to be stored in memory. This places a restriction on training deeper, wider models on single GPU’s(since GPU’s have limited memory) and forces one to use small batch sizes during training. In flow based networks, one does not need to store the activations at all, as they can be reconstructed online during the back-propagation. This property was leveraged in the RevNets paper (2017) which uses invertible residual blocks. Reducing the memory cost of storing activations significantly improve the ability to efficiently train wider and deeper networks.
-
Flowtron (2020), an autoregressive flow based TTS model does a kind of representation learning using normalizing flows to learn an invertible mapping from a data space to a latent space which can be manipulated to control many aspects of speech synthesis (pitch, tone, speech rate, cadence, accent). Flowtron matches state-of-the-art TTS models in terms of speech quality and is able to transfer speech characteristics from a source speaker to a target speaker, making the target speaker sound more expressive.
-
If you’ve ever thought about reversible networks, Normalizing flows do precisely that. Reversibility of flows also means that one can trivially encode images into the latent space for editing. They also have cool mathematical applications, for example their use in Neural ODE solvers (2019.) which use continuous normalizing flows.
Brief Introduction
Definition: A Normalizing Flow is a transformation of a simple probability distribution into a more complex distribution by a sequence of invertible and differentiable mappings.
Note: The above formalism is a simplification, for a more precise definition one can consult [5]. The formalism allows piecewise continuous functions to be used in the construction of the flow which the above definition restricts.
Normalizing since the transformed distribution needs to be normalized by the change of variables formula (discussed below). Flow refers to the series of invertible transformations which are composed with each other to create more complex invertible transformations.
When applied as density estimators, some NFs provide a general way of constructing flexible probability distributions over continuous random variables starting from a simple probability distribution. By constraining the transformations to be invertible, Flow-based models provide a tractable method to calculate the exact likelihood for a wide variety of generative modeling problems.
Efficient inference and efficient synthesis: Autoregressive models, such as the PixelCNN, are also reversible, however synthesis from such models is difficult to parallelize, and typically inefficient on parallel hardware. Flow-based generative models like Glow (and RealNVP) are efficient to parallelize for both training and synthesis.
Exact latent-variable inference: Within the class of exact likelihood models, normalizing flows provide two key advantages: model flexibility and generation speed. Flows have been explored both to increase the flexibility of the variational posterior in the context of variational autoencoders (VAEs), and directly as a generative model. With VAEs, one is able to infer only approximately the value of the latent variables that correspond to a datapoint. GAN’s have no encoder at all to infer the latents. In flow based generative models, this can be done exactly without approximation. Not only does this lead to accurate inference, it also enables optimization of the exact log-likelihood of the data, instead of a lower bound of it.
Mathematical Framework
Let, \(z_0\) be a continuous random variable belonging to a simple probability distribution \(p_\theta(z_0)\) . Let it be a Gaussian with parameters \((\mu, \sigma) = (0,1)\).
\[z_0 \sim p_\theta (z_0) = N(z_0;0,1)\]Normalizing flows transforms the simple distribution, into a desired output probability distribution with random variable \(x\), with a sequence of invertible transformations, \(f_i's\).
\[z_k = f_\theta (z_0) = f_k...f_2.f_1(z_0) \text{ s.t. each $f_i$ is invertible (bijective)}\]The composition of all the individual flows is represented by \(f_\theta\). Since each \(f_i\) is bijective, so is \(f_\theta\). The new density \(p_\theta (z_k)\) is called a push forward of the initial density \(p_\theta(z_0)\) by the function \(f_\theta.\)
An example of a transformation obtained by a normalizing flow is shown below, which transforms a base gaussian distribution into a target multi-modal distribution with the help of a bijective function.
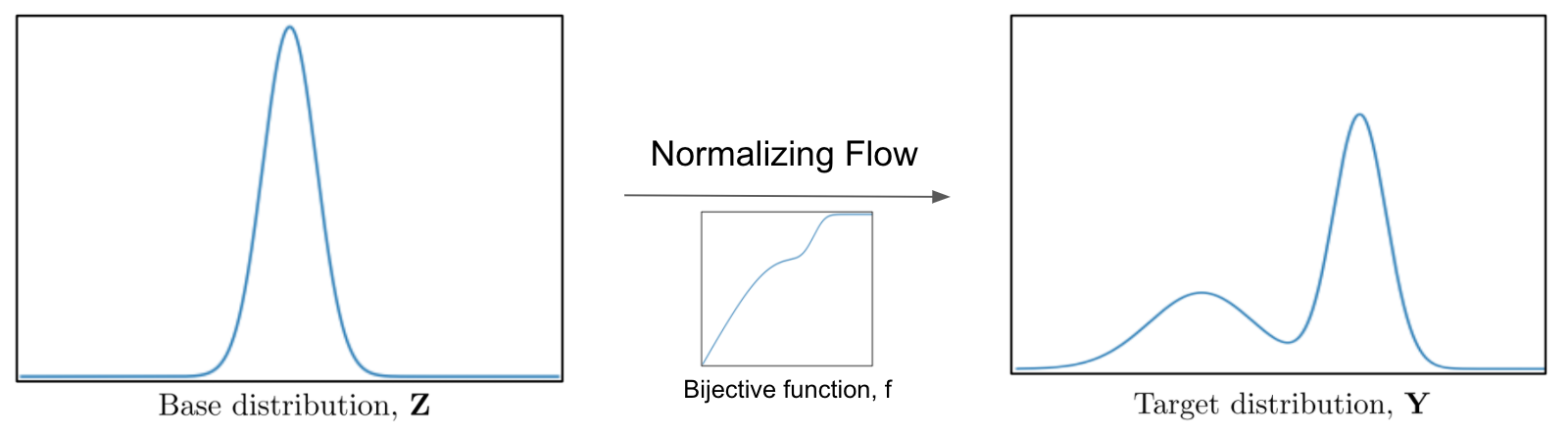
The constrains of a distribution being a probability distribution is that \(\int p_\theta (z_0) =1\). However, this doesn’t hold after applying a bijective function (for intuition consider \(f_1 : z \rightarrow z^3\)).
Change of Variables Formula
Consider the normalizing flow \(f_1 : Z_0 \rightarrow Z_1\). If we want the probability distribution of the random variable \(z_1 \sim Z_1\), we need to consider the change of variables formula derived below.
Consider the event \(z_0 \sim Z\), mapped to \(z_1 \sim Z_1\) s.t. \(f_1(z_0) = z_1\). Since, the mapping is bijective, the probabilities of the events are the same. Therefore,
\[p_\theta(z_1)*\partial z_1 = p_\theta(z_0)*\partial z_0\] \[p_\theta(z_1) = p_\theta(z_0)* \frac{\partial z_0}{\partial z_1}\] \[p_\theta(z_1) = p_\theta(z_0)* |\frac{\partial z_0}{\partial z_1}|\](since probabilities are always > 0)
\[p_\theta(z_1) = p_\theta(z_0)* |\frac{\partial z_0}{\partial f_1(z_0)}|\](\(z_1 = f_1(z_0)\))
\[p_\theta(z_1) = p_\theta(z_0)* |\frac{\partial f_1(z_0)}{\partial z_0}|^{-1}\]In the multivariate case (\(R^D \rightarrow R^D\)) this generalises to:
\[p_\theta(z_1) = p_\theta(z_0)* |\det(\frac{\partial f_1(z_0)}{\partial z_0})|^{-1}\]Considering the sequence of compositional transformations \(f_i's\), one obtains:
\[p_\theta(z_k) = p_\theta(z_0)* \prod_{i=1..k}|\det(\frac{\partial f_i}{\partial z_{i-1}})|^{-1}\]The term on the right i.e. determinant of the Jacobian accounts for the change of \(\delta\) volume induced by the transformation. It serves to normalize the transformed distribution locally, after each flow through a transformation, hence the name, Normalizing Flows.
Some Questions at this stage:
- The sequence of flows need to be invertible and differentiable. What sort of constraints does it introduce in terms of the output distributions that can be reached? Are there families of distributions that we can’t reach starting from a Gaussian?
Sampling
In this case, the bijective functions and the initial distribution are given. Sampling points from the output distribution requires calculating the forward pass, i.e. an efficient calculation of the functions \(f_i's\).
Density Estimation using Maximum Likelihood
In this case a dataset \(\{a_1, a_2,....,a_n\}\) is provided and the objective is to learn the probability density function \(p_\theta(A)\) to which the points belong. An initial density \(p_\theta(z_0)\) is chosen.
For each \(a_i\) we have:
\[p_\theta(a_i) = p_\theta(z_i)* |\det(\frac{\partial f(z_i)}{\partial z_i})|^{-1}\]where, \(a_i = f(z_i)\)
\[\prod_{i=1}^n p_\theta(a_i) =\prod_{i=1}^n [p_\theta(z_i)* |\det(\frac{\partial f(z_i)}{\partial z_i})|^{-1}]\]We need to maximize the above over all possible flows \(f\) to find the flow \(\hat{f}\) that maximizes the probability.
\[\hat{f} =\text{arg max}_f \text{ }\prod_{i=1}^n [p_\theta(z_i)* |\det(\frac{\partial f(z_i)}{\partial z_i})|^{-1}]\]Using log likelihood maximization we arrive at:
\[\hat{f} =\text{arg max}_f \text{ }\sum_{i=1}^n [log(p_\theta(z_i)) - log(|\det(\frac{\partial f(z_i)}{\partial z_i})|)]\]The equation shown above is used during training for density estimation. However, since we only know \(a_i's\) the only way to find \(z_i's\) which are used, is to find the inverse mapping i.e. \(z_i = f^{-1}(a_i)\) . So for density estimation and training, the calculation of both the inverse and determinant of the Jacobian are required.
However, calculating the inverse and the determinant of the Jacobian of a sequence of high dimensional transformations can be very time consuming (for dimensionality \(d\) matrix, both are of complexity \(O(d^3)\)). There are various tricks that are used to reduce the complexity of these two operations, one of the popular ones being the use of triangular maps.
Triangular maps:
Let \(T\) be a normalizing flow, \(T: z \rightarrow x\) where \(x = (x_1, x_2 .... x_d)\) and \(z = (z_1, z_2 .... z_d)\). More generally, one can decompose \(T\) into \(T_1, T_2...T_d\) such that \(x_i = T_i(z_1,z_2.....z_d)\).
Now if we want to introduce an additional constraint on \(T\) i.e. for \(T\) to be a triangular map, each \(T_j\) should be a function of \((z_1,z_2.....z_j)\) i.e. the first \(j\) elements and not all the \(d\) elements.
For triangular maps/matrices, both the inverse and the determinant of the jacobian is easy to compute. The jacobian for a triangular map is shown below. The determinant is simply the product of the diagonals and has a complexity of \(O(d)\) instead of \(O(d^3)\). The complexity for the calculation of the inverse is \(O(d^2)\) instead of \(O(d^3)\).

Note: For an increasing triangular map, \(\frac {\partial T_i}{\partial z_i} > 0\). This will be useful in Part - 2 where the different types/families of Normalizing flows will be considered.